Il piacere di scoprire
Oggi siamo partiti accendendo il pc della maestra ed è apparsa questa immagine del Desktop
![]()
I bambini spontaneamente hanno cominciato ad osservare e commentare riconoscendo un paesaggio geografico.
Poiché il luogo è una località turistica a molti familiare perchè frequentata per le vacanza dai cittadini della nostra città, è stato chiesto se la riconoscevano: Sperlonga.
I bambini allora hanno chiesto da quale punto della cittadina era stata scattata la fotografia e poi hanno cominciato a riconoscere gli elementi presenti nell'immagine, a classificarli in naturali e antropici. Sono andati ad osservare alcuni piccolissimi particolari che non erano ben focalizzati ma si scorgevano piccoli quadratini, così l'occasione per riparlare dei pixel che compongono un'immagine e richiamare alla mente le attività di pixel art realizzate negli anni prcedenti, è stata servita su un piatto d'argento.
A quel punto ho proseguito con la proposta che avevo previsto e per la quale avevo scelto di utilizzare il monitor interattivo: dare avvio alle riflessioni sul percorso che ci attende quest'anno ripercorrendo quanto abbiamo già conosciuto e fatto esperienza nel corso degli anni precedenti.
Il tempo
Ho proposto la visione di questo video sul tempo realizzato da
Planck, rivista scientifica per ragazzi.
https://www.planck-magazine.it/index.php/videoLo abbiamo visionato due volte per prestare attenzione a ciò che ad una prima visione era sfuggito
poi ho chiesto cosa, presente nel video, conoscevano già perché ne avevamo parlato: così la conversazione è andata sulla storia dell'orologio, il movimento apparente del sole e delle stelle, i movimenti della Terra e il modello realizzato da Francesco, il giorno e la notte, l'anno e le stagioni, l'anno bisestile.
https://classeacolori.blogspot.com/2019/03/misurare-il-tempo-lorologio.htmlhttps://classeacolori.blogspot.com/2018/11/i-bambini-realizzano.html
Poi Giacomo ha provato a spiegare ai compagni i movimenti della Terra che avevamo rivisto e mentre lui parlava e faceva esempi per aiutarsi nella spiegazione, io scrivevo alla lavagna ciò che diceva in modo sintetico, utilizzando uno schema.
Alla fine ho chiesto ai bambini di osservare lo schema e vedere se faceva capire in breve quello che Giacomo aveva spiegato.
Ho parlato allora del metodo di studio e degli strumenti per aiutarci a studiare, non uguali per tutti perché ognuno apprende in modo diverso.
Ho detto loro che ognuno dovrà scoprire lo strumento più utile ed efficace!
Poi ci siamo soffermati su ciò che nel video avevano sentito per la prima volta: il tempo e la velocità della luce, i Maya e la fine del mondo, le datazioni nella storia dell'orologio, avanti Cristo e dopo Cristo.
Così si sono toccati diversi temi come l'origine della Terra e il conteggio degli anni, con numeri molto grandi, le bufale, fino ad arrivare alle deepfake (spunto un video trasmesso da Striscia la notizia in prima serata) parlando di intelligenza artificiale che in questo caso ha permesso di manipolare immagini e volti.
Il Big Bang, i primi uomini, la teoria dell'evoluzione...i bambini hanno parlato e raccontato le preconoscenze in loro possesso confrontandosi con i compagni, poi Sara ha detto di aver visitato il MUSE di Trento questa estate: allora abbiamo preso la carta geografica dell'Italia, visto che è divisa in regioni e che Trento si trova nella regione del Trentino alto Adige nel Nord Italia. Poi abbiamo navigato sul sito del MUSE e Sara ci ha spiegato cosa aveva visto nei vari piani del museo mentre passavano le immagini e i contenuti del sito. Ci siamo soffermati sui fossili (cosa ci fanno le conchiglie sulle montagne, anticipando che se lo era chiesto anche Leonardo Da Vinci) e sui ghiacciai e non abbiamo potuto non parlare del problema del loro scioglimento, il riscaldamento globale, i cambiamenti climatici, la manifestazione del 27 settembre, il discorso di Greta alle nazioni unite ascoltato al telegiornale.
Così la conversazione si è arricchita di moltissimi altri contenuti che alla fine abbiamo elencato alla lavagna alla quale Mattia ha scattato una fotografia per poter consultare di nuovo l'elenco nella prossima lezione.
![]()
Sono volate tre ore, tutti si sono meravigliati...e Giulio è andato di corsa al bagno perché fino a quel momento aveva aspettato temendo di perdersi qualcosa!
Come stiamo lavorando con il calcolo
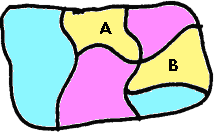Questa mappa è colorata correttamente perché le regioni A e B hanno in comune un solo punto.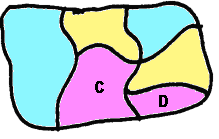
Le dita alzate nella figura, per esempio, rappresentano il numero 5
Dall'Archivio storico di Frosinone
